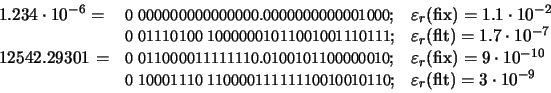Ejemplo

08.05.2015 06:54

Suponga un ordenador cuya notación de punto fijo consiste en palabras de longitud 32 bits repartidas del siguiente modo: 1 bit para el signo, 15 bits para la parte entera y 16 bits para la parte fraccionaria. Represente los números 26.32, 1234x10-4 y 12542.29301 en base 2 empleando esta notación de punto fijo y notación de punto flotante MARC-32 con 32 bits. Calcule el error de almacenamiento cometido en cada caso.

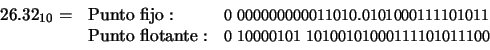
\begin{displaymath}\begin{array}{lll}26.32_{10} = & \mathrm{Punto~fijo:} &\m...... &\mbox{\small0 10000101 10100101000111101011100}\end{array}\end{displaymath}

Si expresamos el error como la diferencia entre el valor y el número realmente almacenado en el ordenador, obtenemos:

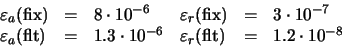
\begin{displaymath}\begin{array}{llllll}\varepsilon_{a}(\mathrm{fix}) & = & 8 ......arepsilon_{r}(\mathrm{flt}) & = & 1.2 \cdot 10^{-8}\end{array}\end{displaymath}

En cuanto a los otros dos números, obtenemos:

\begin{displaymath}\begin{array}{lll}1.234 \cdot 10^{-6} = & \mbox{\small0 000...... &\varepsilon_{r}(\mathrm{flt}) = 3 \cdot 10^{-9}\end{array}\end{displaymath}

 

 

 

Volver